Python資料科學學習手冊學習筆記 (4) Scikit-Learn - 監督式學習相關演算法

　　不同於先前介紹NumPy、Pandas與Matplotlib等套件時較為混亂的編排，這本由Jake VanderPlas著作，何敏煌譯著的《Python資料科學學習手冊》(Python Data Science Handbook: Essential Tools for Working with Data)，在引領讀者探索機器學習領域時，使用口語化、系統化的方式進行說明，如果您對機器學習沒有基礎概念，可以考慮從本書讀起，但是先決條件是必須先熟悉NumPy、Pandas與Matplotlib等套件。

　　本書的機器學習篇幅全數在第五章，以Scikit-Learn套件實作並介紹：一、機器學習基本術語和概念；二、常見演算法的原理；三、透過各式應用範例，討論如何選擇使用不同的演算法，與各式功能的調整、判斷。讀完此章節之後，對於簡單的資料集，應該有基本的判斷與處理能力，但對於現實應用，則仍有更多的問題有待解決，需要精進技能並結合更多工具才行。

　　距離上一次張貼資料科學相關網誌已有好幾個月的時間，除了本人生活忙碌，更主要的原因是機器學習對於非資訊、統計相關背景的人來說，是一門不容易駕馭的知識技術，面對如此陡峭的學習曲線，需要投資不少時間與心力理解其中的繁瑣細節，不過所幸本書對於機器學習章節的編排，讓我於研讀的過程，有如初學Python程式語言一般，能夠循序漸進地駕馭這門學問。

第五章：機器學習

深入探究－迴歸－迴歸(Regression)

l   簡單線性迴歸(Simple Linear Regression)：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
x = 10 * np.random.rand(50)
y = 2 * x - 1 + np.random.randn(50)
x_fit = np.linspace(-1, 11)

# 套用Estimator
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept = True)
y_fit = model.fit(x[:, np.newaxis], y).predict(x_fit[:, np.newaxis])

# 繪圖
plt.scatter(x, y)
plt.plot(x_fit, y_fit)
plt.show()

l   高斯過程迴歸(Gaussian Process Regression)：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
def make_data(N, err = 1, rseed = 1):
    rng = np.random.RandomState(rseed)
    X = rng.rand(N, 1) ** 2
    y = 10 - 1 / (X.ravel() + 0.1)
    if err > 0:
        y += err * rng.randn(N)
    return X, y
X, y = make_data(40)
x_fit = np.linspace(0, 1, 1000)

# 套用Estimator
from sklearn.gaussian_process import GaussianProcessRegressor
model = GaussianProcessRegressor()
y_fit = model.fit(X, y).predict(x_fit[:, np.newaxis])

# 繪圖
plt.scatter(X, y)
plt.plot(x_fit, y_fit)
plt.fill_between(x_fit.ravel(), y_fit - 2, y_fit + 2, alpha = 0.2)
plt.xlim(-0.2, 1.2)
plt.show()

l   多項式基函數(Polynomial Basis Functions)：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
rng = np.random.RandomState(0)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
x_fit = np.linspace(0, 10, 1000)

# 套用Estimator
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
model = make_pipeline(PolynomialFeatures(7), LinearRegression())
y_fit = model.fit(x[:, np.newaxis], y).predict(x_fit[:, np.newaxis])

# 繪圖
plt.scatter(x, y)
plt.plot(x_fit, y_fit)
plt.show()

l   高斯基函數(Gaussian Basis Functions)並沒有內建在Scikit-Learn，但是可以編寫自訂轉換器來建立：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
rng = np.random.RandomState(0)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
x_fit = np.linspace(0, 10, 1000)

# Scikit-Learn Estimator被以Python的類別來實作
from sklearn.base import BaseEstimator, TransformerMixin
class GaussianFeatures(BaseEstimator, TransformerMixin):
    def __init__(self, N, width_factor = 2.0):
        self.N = N
        self.width_factor = width_factor
    # decorator
    @staticmethod
    def _gauss_basis(x, y, width, axis = None):
        arg = (x - y) / width
        return np.exp(-0.5 * np.sum(arg ** 2, axis))
    def fit(self, X, y = None):
        # create N centers spread along the data range
        self.centers_ = np.linspace(X.min(), X.max(), self.N)
        self.width_ = self.width_factor * (self.centers_[1] - self.centers_[0])
        return self
    def transform(self, X):
        return self._gauss_basis(X[:, :, np.newaxis], self.centers_, self.width_, axis = 1)

# 套用Estimator
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
model = make_pipeline(GaussianFeatures(10), LinearRegression())
y_fit = model.fit(x[:, np.newaxis], y).predict(x_fit[:, np.newaxis])

# 繪圖
fig, ax = plt.subplots(2, sharex = True)
ax[0].scatter(x, y)
ax[0].plot(x_fit, y_fit)
# 畫出高斯基中心與係數的相應位置
ax[1].plot(model.steps[0][1].centers_, model.steps[1][1].coef_)
ax[1].set(xlabel = "Basis Location", ylabel = "Coefficinet")
plt.show()

l   正規化(Regularization)藉由處罰模型參數中那些過大的值來限制在模型中明顯的突波，以上述高斯基函數(Gaussian Basis Functions)為範例，替換程式碼中套用Estimator的部份：

Ridge Regression(L₂ Regularization, Tikhonov正規化)處罰模型係數的平方和(2-norms)，其中alpha是一個自由的參數，用來控制處罰的強度：
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Ridge
model = make_pipeline(GaussianFeatures(30), Ridge(alpha = 0.1))
y_fit = model.fit(x[:, np.newaxis], y).predict(x_fit[:, np.newaxis])

Lasso Regularization(L₁ Regularization)處罰迴歸係數的絕對值和(1-norms)，此種方式較利於分散模型，因為它會優先把模型係數設定到剛好為0：
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Lasso
model = make_pipeline(GaussianFeatures(30), Lasso(alpha = 0.001))
y_fit = model.fit(x[:, np.newaxis], y).predict(x_fit[:, np.newaxis])

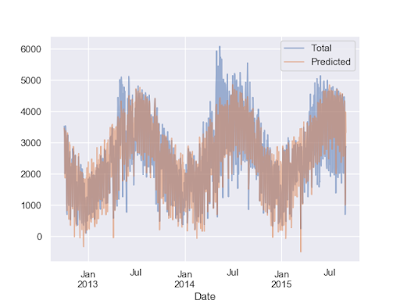
l   範例－預測自行車的流量：
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 原始資料
# https://data.seattle.gov/Transportation/Fremont-Bridge-Hourly-Bicycle-Counts-by-Month-Octo/65db-xm6k
counts = pd.read_csv("Fremont_Bridge.csv", index_col = "Date", parse_dates = True)
weather = pd.read_csv("BicycleWeather.csv", index_col = "DATE", parse_dates = True)

# 資料處理－計算每天的自行車總流量
daily = counts.resample("d").sum()
daily["Total"] = daily.sum(axis = 1)
daily = daily[["Total"]]

# 資料處理－僅使用同時有自行車流量與氣象紀錄的日期
daily = daily.loc[pd.to_datetime("2012/10/03"):pd.to_datetime("2015/09/01")]

# 資料處理－記錄星期幾
days = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"]
for i in range(7):
    daily[days[i]] = (daily.index.dayofweek == i).astype(float)

# 資料處理－記錄美國假日
from pandas.tseries.holiday import USFederalHolidayCalendar
holidays = USFederalHolidayCalendar().holidays("2012", "2019")
daily = daily.join(pd.Series(1, index = holidays, name = "Holiday"))
daily["Holiday"].fillna(0, inplace = True)

# 資料處理－記錄白晝的小時數，使用標準的天文學運算
def hours_of_daylight(date, axis = 23.44, latitude = 47.61):
    days = (date - pd.datetime(2000, 12, 21)).days
    m = (1 - np.tan(np.radians(latitude)) * np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25)))
    return 24 * np.degrees(np.arccos(1 - np.clip(m, 0, 2))) / 180
daily["Daylight_Hrs"] = list(map(hours_of_daylight, daily.index))

# 資料處理－加上平均溫度和總降雨量
# 溫度單位為0.1度C，轉換為C
weather["TMIN"] /= 10
weather["TMAX"] /= 10
weather["Temp (C)"] = 0.5 * (weather["TMIN"] + weather["TMAX"])
# 雨量單位為0.1毫米，轉換為英吋
weather["PRCP"] /= 254
weather["Dry Day"] = (weather["PRCP"] == 0).astype(int)
daily = daily.join(weather[["Temp (C)", "PRCP", "Dry Day"]])

# 資料處理－計算總共過了多少年
daily["Annual"] = (daily.index - daily.index[0]).days / 365

# 進行機器學習，使用簡單線性迴歸(Simple Linear Regression)
# 資料
column_names = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun", "Holiday", "Daylight_Hrs", "PRCP", "Dry Day", "Temp (C)", "Annual"]
X = daily[column_names]
y = daily["Total"]

# 套用Estimator
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept = False)
daily["Predicted"] = model.fit(X, y).predict(X)

# 看結果
# 每多出1小時白晝，會多出129人騎自行車
params = pd.Series(model.coef_, index = X.columns)
print(params)

# 以Bootstrap Resampling計算標準差，再看一次結果
# 每多出1小時白晝，會多出129+-9人騎自行車
from sklearn.utils import resample
np.random.seed(0)
err = np.std([model.fit(*resample(X, y)).coef_ for i in range(1000)], axis = 0)
print(pd.DataFrame({"Effect": params.round(0), "Error": err.round(0)}))

# 繪圖
daily[["Total", "Predicted"]].plot(alpha = 0.5)
plt.show()

深入探究－迴歸、分類－支持向量機(Support Vector Machines, SVMs)

l   支持向量機目的為最大化邊界，因此只有那些支持向量(Support Vectors)的位置是相關的，任何遠離邊界的資料點並不會影響擬合結果：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples = 50, centers = 2, random_state = 0, cluster_std = 0.6)

# 套用Estimator
from sklearn.svm import SVC
# C參數用來控制邊界的銳利度
model = SVC(kernel = "linear", C = 1E10)
model.fit(X, y)

# 繪圖
def plot_svc_decision_function(model, ax = None, plot_support = True):
    # 取得繪圖格線
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
   
    # 建立grid以評估模型
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    X, Y = np.meshgrid(x, y)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
   
    # 繪出決策邊界
    ax.contour(X, Y, P, colors = "k", levels = [-1, 0, 1], alpha = 0.5, linestyles = ["--", "-", "--"])
   
    # 繪出支持向量
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s = 100, linewidth = 2, edgecolor = "k", facecolor = "none")

plt.scatter(X[:, 0], X[:, 1], c = y, cmap = "RdBu")
plot_svc_decision_function(model)
plt.show()

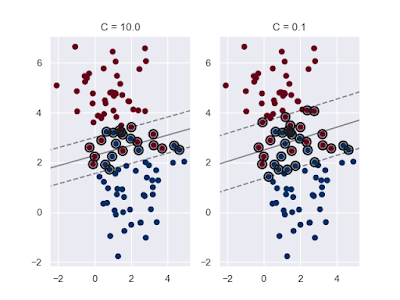
l   模糊因子(Fudge-Factor)可以用來柔化邊界，若C參數很大，邊界就很銳利，而C參數最佳的值需由資料集決定，應該透過交叉驗證或是類似的程序來調整：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples = 100, centers = 2, random_state = 0, cluster_std = 1.2)

# 套用Estimator並繪圖比較
from sklearn.svm import SVC

def plot_svc_decision_function(model, ax = None, plot_support = True):
    # 取得繪圖格線
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
   
    # 建立grid以評估模型
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    X, Y = np.meshgrid(x, y)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
   
    # 繪出決策邊界
    ax.contour(X, Y, P, colors = "k", levels = [-1, 0, 1], alpha = 0.5, linestyles = ["--", "-", "--"])
   
    # 繪出支持向量
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s = 100, linewidth = 2, edgecolor = "k", facecolor = "none")

fig, ax = plt.subplots(1, 2)
for axi, C in zip(ax, [10.0, 0.1]):
    model = SVC(kernel = "linear", C = C)
    model.fit(X, y)
    axi.set_title("C = " + str(C))
    axi.scatter(X[:, 0], X[:, 1], c = y, cmap = "RdBu")
    plot_svc_decision_function(model, ax = axi)
plt.show()

l   核轉換(Kernel Transformation)－使用核心技巧(Kernel Trick)，改變線性核心到適用此例的RBF(Radial Basis Function)核心：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets.samples_generator import make_circles
X, y = make_circles(n_samples = 100, factor = 0.1, noise = 0.1, random_state = 0)

# 套用Estimator
from sklearn.svm import SVC
# gamma參數用來控制Radial Basis Function Kernel的大小
model = SVC(kernel = "rbf", C = 1E6, gamma = "auto")
model.fit(X, y)

# 繪圖
def plot_svc_decision_function(model, ax = None, plot_support = True):
    # 取得繪圖格線
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
   
    # 建立grid以評估模型
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    X, Y = np.meshgrid(x, y)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
   
    # 繪出決策邊界
    ax.contour(X, Y, P, colors = "k", levels = [-1, 0, 1], alpha = 0.5, linestyles = ["--", "-", "--"])
   
    # 繪出支持向量
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s = 100, linewidth = 2, edgecolor = "k", facecolor = "none")

plt.scatter(X[:, 0], X[:, 1], c = y, cmap = "RdBu")
plot_svc_decision_function(model)
plt.show()

l   範例－人臉辨識：
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
faces = fetch_lfw_people(min_faces_per_person = 60)
X_train, X_test, y_train, y_test = train_test_split(faces.data, faces.target, random_state = 0)

# 套用Estimator
# 通常使用預處理器萃取出一些比較有意義的特徵效果會更好
from sklearn.decomposition import PCA
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
model_pca = PCA(n_components = 150, whiten = True, random_state = 0)
model_svc = SVC(kernel = "rbf", class_weight = "balanced")
model = make_pipeline(model_pca, model_svc)

# 格狀搜尋
from sklearn.model_selection import GridSearchCV
param_grid = {"svc__C": [1, 5, 10, 50], "svc__gamma": [0.0001, 0.0005, 0.001, 0.005]}
grid = GridSearchCV(model, param_grid)
grid.fit(X_train, y_train)
grid_model = grid.best_estimator_
y_fit = grid_model.predict(X_test)

# 分類報告
from sklearn.metrics import classification_report
print(classification_report(y_test, y_fit, target_names = faces.target_names))

# 混淆矩陣繪圖
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(y_test, y_fit)
sns.heatmap(mat.T, square = True, annot = True, fmt = "d", cbar = False, xticklabels = faces.target_names, yticklabels = faces.target_names)
plt.xlabel("True Label")
plt.ylabel("Predicted Label")
plt.show()

# 檢視結果繪圖
fig, ax = plt.subplots(4, 6)
for i, axi in enumerate(ax.flat):
    axi.imshow(X_test[i].reshape(faces.images.shape[1], faces.images.shape[2]))
    axi.set(xticks = [], yticks = [])
    axi.set_xlabel(faces.target_names[y_fit[i]], color = "black" if y_fit[i] == y_test[i] else "red", size = 6)
fig.suptitle("Predicted Names; Incorrect Labels in Red", size = 12)
plt.show()

l   使用支持向量機分類器的優缺點：
優點一－依賴相對少的支持向量
優點二－預測階段的速度非常快
優點三－在高維度資料中運作好
優點四－核方法整合非常多樣化
缺點一－大訓練樣本的計算成本可能太高
缺點二－非常依賴一個合適的柔化參數C
缺點三－運算結果沒有直接的機率學解釋

深入探究－迴歸、分類－決策樹(Decision Tree)和隨機森林(Random Forest)

l   隨機森林是建立在決策樹上的一個整體學習法(Ensemble)：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples = 300, centers = 4, random_state = 0, cluster_std = 1.0)

# 套用Estimator
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
model.fit(X, y)

# 繪圖
def visualize_classifier(model, y_classes):
    # 取得繪圖格線
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
   
    # 建立grid以評估模型
    x = np.linspace(xlim[0], xlim[1], 200)
    y = np.linspace(ylim[0], ylim[1], 200)
    X, Y = np.meshgrid(x, y)
    xy = np.c_[X.ravel(), Y.ravel()]
    Z = model.predict(xy).reshape(X.shape)
   
    # 繪出決策邊界
    n_classes = len(np.unique(y_classes))
    ax.contourf(X, Y, Z, alpha = 0.25, levels = np.arange(n_classes + 1) - 0.5, cmap = "rainbow")

plt.scatter(X[:, 0], X[:, 1], c = y, cmap = "rainbow")
visualize_classifier(model, y)
plt.show()

l   過度擬合是決策樹的一般特性，若同時使用這些決策樹的評估結果，就可以得到比單一決策樹還要好的評估結果，而集成評估器的基本概念就是Bagging集成方法：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples = 300, centers = 4, random_state = 0, cluster_std = 1.0)

# 套用Estimator
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
model_tree = DecisionTreeClassifier()
# 實務上選用隨機子集合會讓決策樹更有效率
model_bag = BaggingClassifier(model_tree, n_estimators = 100, max_samples = 0.8, random_state = 0)
model_bag.fit(X, y)

# 繪圖
def visualize_classifier(model, y_classes):
    # 取得繪圖格線
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
   
    # 建立grid以評估模型
    x = np.linspace(xlim[0], xlim[1], 200)
    y = np.linspace(ylim[0], ylim[1], 200)
    X, Y = np.meshgrid(x, y)
    xy = np.c_[X.ravel(), Y.ravel()]
    Z = model.predict(xy).reshape(X.shape)
   
    # 繪出決策邊界
    n_classes = len(np.unique(y_classes))
    ax.contourf(X, Y, Z, alpha = 0.25, levels = np.arange(n_classes + 1) - 0.5, cmap = "rainbow")

plt.scatter(X[:, 0], X[:, 1], c = y, cmap = "rainbow")
visualize_classifier(model_bag, y)
plt.show()

l   最佳化的隨機森林評估器以RandomForestClassifier實作，它會自動處理隨機程序的所有細節：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples = 300, centers = 4, random_state = 0, cluster_std = 1.0)

# 套用Estimator
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators = 100, random_state = 0)
model.fit(X, y)

# 繪圖
def visualize_classifier(model, y_classes):
    # 取得繪圖格線
    ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
   
    # 建立grid以評估模型
    x = np.linspace(xlim[0], xlim[1], 200)
    y = np.linspace(ylim[0], ylim[1], 200)
    X, Y = np.meshgrid(x, y)
    xy = np.c_[X.ravel(), Y.ravel()]
    Z = model.predict(xy).reshape(X.shape)
   
    # 繪出決策邊界
    n_classes = len(np.unique(y_classes))
    ax.contourf(X, Y, Z, alpha = 0.25, levels = np.arange(n_classes + 1) - 0.5, cmap = "rainbow")

plt.scatter(X[:, 0], X[:, 1], c = y, cmap = "rainbow")
visualize_classifier(model, y)
plt.show()

l   隨機森林迴歸(Random Forest Regression)：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
rng = np.random.RandomState(0)
x = 10 * rng.rand(200)
y = np.sin(0.5 * x) + np.sin(5 * x) + 0.3 * rng.randn(len(x))
x_fit = np.linspace(0, 10, 1000)

# 套用Estimator
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators = 200)
y_fit = model.fit(x[:, np.newaxis], y).predict(x_fit[:, np.newaxis])

# 繪圖
plt.errorbar(x, y, 0.3, fmt = "o", alpha = 0.5)
plt.plot(x_fit, y_fit, "-r")
plt.show()

l   範例－手寫數字分類：
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits()
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, random_state = 0)

# 套用Estimator
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators = 1000)
model.fit(X_train, y_train)
y_fit = model.predict(X_test)

# 分類報告
from sklearn.metrics import classification_report
print(classification_report(y_test, y_fit))
# 機率
print(model.predict_proba(X_test))

# 繪圖
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(y_test, y_fit)
sns.heatmap(mat.T, square = True, annot = True, fmt = "d", cbar = False)
plt.xlabel("True Label")
plt.ylabel("Predicted Label")
plt.show()

l   使用隨機森林分類器的優缺點：
優點一－可以平行化處理每一棵決策樹，訓練與預測都非常快速
優點二－因為進行過半數投票，有機率分類意義
優點三－無母數模型非常具有彈性
缺點一－評估的結果不容易被解釋

深入探究－分類－樸素貝氏分類法(Naive Bayes Classification)

l   高斯樸素貝氏(Gaussian Naive Bayes)這個分類器假設每一個標籤的資料都是來自於簡單高斯分佈(Simple Gaussian Distribution, 常態分佈)：
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples = 100, n_features = 2, centers = 2, random_state = 0, cluster_std = 1.5)
rng = np.random.RandomState(0)
X_fit = [-6, -14] + [18, 21] * rng.rand(2000, 2)

# 套用Estimator
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
y_fit = model.fit(X, y).predict(X_fit)

# 後驗機率(Posterior Probabilities)
y_prob = model.predict_proba(X_fit)
print(y_prob[-8:].round(2))

# 繪圖
plt.scatter(X[:, 0], X[:, 1], c = y, s = 50, cmap = "RdBu")
plt.scatter(X_fit[:, 0], X_fit[:, 1], c = y_fit, s = 20, cmap = "RdBu", alpha = 0.2)
plt.show()

l   多項式樸素貝氏(Multinomial Naive Bayes)這個分類器假設每一個標籤的資料都是來自於簡單多項式分佈(Multinomial Distribution)，適合用於計次，以下是文字分類範例：
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import fetch_20newsgroups
# print(fetch_20newsgroups().target_names)，從中選用部分類別
categories = ["talk.religion.misc", "soc.religion.christian", "sci.space", "comp.graphics"]
train = fetch_20newsgroups(subset = "train", categories = categories)
test = fetch_20newsgroups(subset = "test", categories = categories)

# 特徵工程、套用Estimator
from sklearn.pipeline import make_pipeline
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
model = make_pipeline(TfidfVectorizer(), MultinomialNB())
predicted_labels = model.fit(train.data, train.target).predict(test.data)

# 繪圖
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(test.target, predicted_labels)
sns.heatmap(mat.T, square = True, annot = True, fmt = "d", cbar = False, xticklabels = train.target_names, yticklabels = train.target_names)
plt.xlabel("True Label")
plt.ylabel("Predicted Label")
plt.show()

# 快速的工具函式，可以傳回單一字串的預測結果
def predict_category(s, train = train, model = model):
    pred = model.predict([s])
    return train.target_names[pred[0]]
print(predict_category("sending a payload to the ISS"))
print(predict_category("discussing islam vs atheism"))
print(predict_category("determining the screen resolution"))

l   使用樸素貝氏分類器的時機：
優點一－訓練或預測非常快速
優點二－提供直覺的機率預測
優點三－通常都非常易於解讀
優點四－可調變的參數非常少

l   樸素貝氏分類器通常在以下的情況成立時會表現地特別好：
情況一－當資料正好符合樸素(Naive)的假設時
情況二－對於分隔地非常好的類別，模型的複雜度就顯得不是那麼重要
情況三－對於非常高維度的資料，模型的複雜度也顯得不是那麼重要

深入探究－分類－k-近鄰演算法(k-nearest Neighbors, KNN)

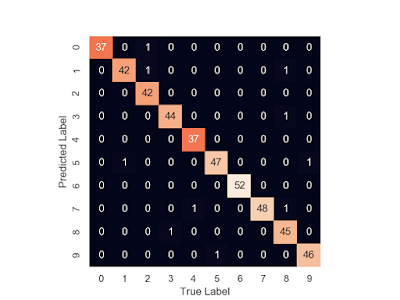
l   k-近鄰演算法(k-nearest Neighbors, KNN)：
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()

# 資料
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits()
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, random_state = 0, train_size = 0.5)

# 套用Estimator
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors = 1)
y_fit = model.fit(X_train, y_train).predict(X_test)

# 準確率
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_fit))

# 繪圖
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(y_test, y_fit)
sns.heatmap(mat.T, square = True, annot = True, fmt = "d", cbar = False)
plt.xlabel("True Label")
plt.ylabel("Predicted Label")
plt.show()