本書的機器學習篇幅全數在第五章,以Scikit-Learn套件實作並介紹:一、機器學習基本術語和概念;二、常見演算法的原理;三、透過各式應用範例,討論如何選擇使用不同的演算法,與各式功能的調整、判斷。讀完此章節之後,對於簡單的資料集,應該有基本的判斷與處理能力,但對於現實應用,則仍有更多的問題有待解決,需要精進技能並結合更多工具才行。
距離上一次張貼資料科學相關網誌已有好幾個月的時間,除了本人生活忙碌,更主要的原因是機器學習對於非資訊、統計相關背景的人來說,是一門不容易駕馭的知識技術,面對如此陡峭的學習曲線,需要投資不少時間與心力理解其中的繁瑣細節,不過所幸本書對於機器學習章節的編排,讓我於研讀的過程,有如初學Python程式語言一般,能夠循序漸進地駕馭這門學問。
第五章:機器學習
本章涵蓋的機器學習種類
l 監督式學習(Supervised Learning):
迴歸(Regression):預測連續性的標籤
迴歸(Regression)
支持向量機(Support Vector Machines, SVMs)
隨機森林分類法(Random Forest Classification)
決策樹(Decision Trees)
隨機森林(Random Forests)
分類(Classification):預測離散的標籤
高斯單純貝氏(Gaussian Naive Bayes)
k-近鄰演算法(k-nearest Neighbors, KNN)
支持向量機(Support Vector Machines, SVMs)
隨機森林分類法(Random Forest Classification)
決策樹(Decision Trees)
隨機森林(Random Forests)
迴歸(Regression):預測連續性的標籤
迴歸(Regression)
支持向量機(Support Vector Machines, SVMs)
隨機森林分類法(Random Forest Classification)
決策樹(Decision Trees)
隨機森林(Random Forests)
分類(Classification):預測離散的標籤
高斯單純貝氏(Gaussian Naive Bayes)
k-近鄰演算法(k-nearest Neighbors, KNN)
支持向量機(Support Vector Machines, SVMs)
隨機森林分類法(Random Forest Classification)
決策樹(Decision Trees)
隨機森林(Random Forests)
l 非監督式學習(Unsupervised Learning):
維度降低(Dimensionality Reduction):未標籤資料的結構推理
主成分分析(Principal Component Analysis, PCA)
流形學習(Manifold Learning)
多維標度(Multidimensional Scaling, MDS)
區域線性嵌入(Locally Linear Embedding, LLE)
等距特徵映射(Isomap)
集群(Clustering):在未建立標籤的資料中推理標籤
k-平均集群法(k-means Clustering)
高斯混合模型(Gaussian Mixture Models, GMM)
維度降低(Dimensionality Reduction):未標籤資料的結構推理
主成分分析(Principal Component Analysis, PCA)
流形學習(Manifold Learning)
多維標度(Multidimensional Scaling, MDS)
區域線性嵌入(Locally Linear Embedding, LLE)
等距特徵映射(Isomap)
集群(Clustering):在未建立標籤的資料中推理標籤
k-平均集群法(k-means Clustering)
高斯混合模型(Gaussian Mixture Models, GMM)
Scikit-Learn機器學習範例
l Scikit-Learn中的資料表示法:
# 會把這個矩陣的所有列稱為樣本(Sample)
# 會把這個矩陣的所有欄稱為特徵(Feature)
import seaborn as sns
iris = sns.load_dataset("iris")
print(iris.head())
# X是特徵矩陣(Feature Matrix),含有樣本(Sample)與特徵(Feature)
# y是目標陣列、目標向量或標籤(Label)
X_iris = iris.drop("species", axis = 1)
print(X_iris.head())
y_iris = iris["species"]
print(y_iris.head())
# 會把這個矩陣的所有列稱為樣本(Sample)
# 會把這個矩陣的所有欄稱為特徵(Feature)
import seaborn as sns
iris = sns.load_dataset("iris")
print(iris.head())
# X是特徵矩陣(Feature Matrix),含有樣本(Sample)與特徵(Feature)
# y是目標陣列、目標向量或標籤(Label)
X_iris = iris.drop("species", axis = 1)
print(X_iris.head())
y_iris = iris["species"]
print(y_iris.head())
l 監督式學習-迴歸-簡單線性迴歸(Simple Linear Regression):
# 資料
import numpy as np
x = 10 * np.random.rand(50)
y = 2 * x - 1 + np.random.randn(50)
# 把資料依特徵矩陣和目標向量的形狀調整
X = x[:, np.newaxis]
# print(X.shape),特徵矩陣的形狀要是(50, 1),而不要是(50,)
# print(y.shape),目標向量的形狀可為(50,),不需調整
# 套用Scikit-Learn Estimator API
# 步驟一-選擇一個模型的類別
from sklearn.linear_model import LinearRegression
# 步驟二-選用模型的超參數(Hyperparameter)
model = LinearRegression(fit_intercept = True)
# 步驟三-擬合模型到資料中
model.fit(X, y)
# print(model.coef_),擬合之斜率
# print(model.intercept_),擬合之截距
# 解釋模型參數是統計問題而不是機器學習問題,如果想要了解模型參數意義,建議使用StatsModels等套件
# 步驟四-預測未知資料的標籤
x_fit = np.linspace(-1, 11)
X_fit = x_fit[:, np.newaxis]
y_fit = model.predict(X_fit)
# 檢視預測的模型和原始的資料之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(x, y)
plt.plot(x_fit, y_fit)
plt.show()
# 資料
import numpy as np
x = 10 * np.random.rand(50)
y = 2 * x - 1 + np.random.randn(50)
# 把資料依特徵矩陣和目標向量的形狀調整
X = x[:, np.newaxis]
# print(X.shape),特徵矩陣的形狀要是(50, 1),而不要是(50,)
# print(y.shape),目標向量的形狀可為(50,),不需調整
# 套用Scikit-Learn Estimator API
# 步驟一-選擇一個模型的類別
from sklearn.linear_model import LinearRegression
# 步驟二-選用模型的超參數(Hyperparameter)
model = LinearRegression(fit_intercept = True)
# 步驟三-擬合模型到資料中
model.fit(X, y)
# print(model.coef_),擬合之斜率
# print(model.intercept_),擬合之截距
# 解釋模型參數是統計問題而不是機器學習問題,如果想要了解模型參數意義,建議使用StatsModels等套件
# 步驟四-預測未知資料的標籤
x_fit = np.linspace(-1, 11)
X_fit = x_fit[:, np.newaxis]
y_fit = model.predict(X_fit)
# 檢視預測的模型和原始的資料之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(x, y)
plt.plot(x_fit, y_fit)
plt.show()
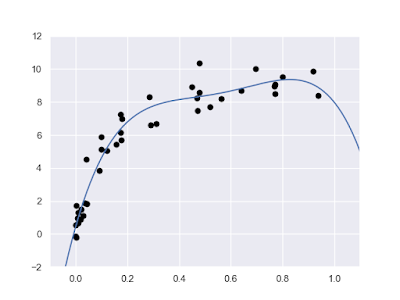
l 監督式學習-迴歸-高斯過程迴歸(Gaussian Process Regression):
# 資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
x_fit = np.linspace(0, 1, 1000)
X_fit = x_fit[:, np.newaxis]
# 套用Scikit-Learn Estimator API
from sklearn.gaussian_process import GaussianProcessRegressor
model = GaussianProcessRegressor()
model.fit(X, y)
y_fit = model.predict(X_fit)
# 檢視預測的模型和原始的資料之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X, y)
plt.plot(x_fit, y_fit)
plt.fill_between(x_fit, y_fit - 2, y_fit + 2, alpha = 0.2)
plt.xlim(-0.2, 1.2)
plt.show()
# 資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
x_fit = np.linspace(0, 1, 1000)
X_fit = x_fit[:, np.newaxis]
# 套用Scikit-Learn Estimator API
from sklearn.gaussian_process import GaussianProcessRegressor
model = GaussianProcessRegressor()
model.fit(X, y)
y_fit = model.predict(X_fit)
# 檢視預測的模型和原始的資料之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X, y)
plt.plot(x_fit, y_fit)
plt.fill_between(x_fit, y_fit - 2, y_fit + 2, alpha = 0.2)
plt.xlim(-0.2, 1.2)
plt.show()
l 監督式學習-分類-高斯單純貝氏(Gaussian Naive Bayes):
"""
# 查看手寫字元圖檔資料
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
print(digits.images.shape)
print(X_digits.shape)
print(y_digits.shape)
fig, axes = plt.subplots(10, 10, figsize = (8, 8), subplot_kw = {"xticks": [], "yticks": []}, gridspec_kw = {"hspace": 0.1, "wspace": 0.1})
for i, ax in enumerate(axes.flat):
ax.imshow(digits.images[i], cmap = "binary")
ax.text(0.05, 0.05, str(digits.target[i]), transform = ax.transAxes, color = "green")
plt.show()
"""
# 資料
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
# 把資料分為訓練集(Training Set)與測試集(Testing Set)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_digits, y_digits, random_state = 0)
# 套用Scikit-Learn Estimator API
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train, y_train)
y_fit = model.predict(X_test)
# 檢視預測的標籤和真正的標籤符合之比率
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_fit))
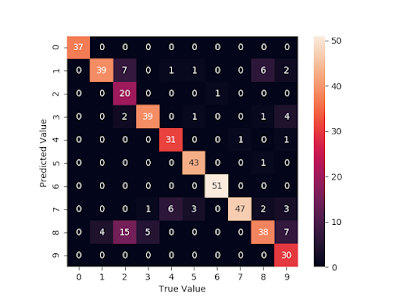
# 混淆矩陣(Confusion Matrix)繪圖
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(y_test, y_fit)
import matplotlib.pyplot as plt
import seaborn as sns
sns.heatmap(mat.T, square = True, annot = True)
plt.xlabel("True Value")
plt.ylabel("Predicted Value ")
plt.show()
"""
# 查看手寫字元圖檔資料
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
print(digits.images.shape)
print(X_digits.shape)
print(y_digits.shape)
fig, axes = plt.subplots(10, 10, figsize = (8, 8), subplot_kw = {"xticks": [], "yticks": []}, gridspec_kw = {"hspace": 0.1, "wspace": 0.1})
for i, ax in enumerate(axes.flat):
ax.imshow(digits.images[i], cmap = "binary")
ax.text(0.05, 0.05, str(digits.target[i]), transform = ax.transAxes, color = "green")
plt.show()
"""
# 資料
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
# 把資料分為訓練集(Training Set)與測試集(Testing Set)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_digits, y_digits, random_state = 0)
# 套用Scikit-Learn Estimator API
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train, y_train)
y_fit = model.predict(X_test)
# 檢視預測的標籤和真正的標籤符合之比率
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_fit))
# 混淆矩陣(Confusion Matrix)繪圖
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(y_test, y_fit)
import matplotlib.pyplot as plt
import seaborn as sns
sns.heatmap(mat.T, square = True, annot = True)
plt.xlabel("True Value")
plt.ylabel("Predicted Value ")
plt.show()
l 非監督式學習-維度降低-主成分分析(Principal Component Analysis, PCA):
# 資料
import seaborn as sns
iris = sns.load_dataset("iris")
X_iris = iris.drop("species", axis = 1)
y_iris = iris["species"]
# 套用Scikit-Learn Estimator API
from sklearn.decomposition import PCA
model = PCA(n_components = 2)
model.fit(X_iris)
X_projected = model.transform(X_iris)
# 檢視預測的成分和真正的類別之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
iris["PCA1"] = X_projected[:, 0]
iris["PCA2"] = X_projected[:, 1]
sns.lmplot("PCA1", "PCA2", hue = "species", data = iris, fit_reg = False)
plt.show()
# 資料
import seaborn as sns
iris = sns.load_dataset("iris")
X_iris = iris.drop("species", axis = 1)
y_iris = iris["species"]
# 套用Scikit-Learn Estimator API
from sklearn.decomposition import PCA
model = PCA(n_components = 2)
model.fit(X_iris)
X_projected = model.transform(X_iris)
# 檢視預測的成分和真正的類別之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
iris["PCA1"] = X_projected[:, 0]
iris["PCA2"] = X_projected[:, 1]
sns.lmplot("PCA1", "PCA2", hue = "species", data = iris, fit_reg = False)
plt.show()
l 非監督式學習-維度降低-流形學習(Manifold Learning)-等距特徵映射(Isomap):
# 資料
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
# 套用Scikit-Learn Estimator API
from sklearn.manifold import Isomap
model = Isomap(n_components = 2)
model.fit(X_digits)
X_projected = model.transform(X_digits)
# 檢視預測的成分和真正的類別之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X_projected[:, 0], X_projected[:, 1], c = y_digits, edgecolor = "none", alpha = 0.5, cmap = plt.cm.get_cmap("cubehelix", 10))
plt.colorbar(label = "Digit Label", ticks = range(10))
plt.clim(-0.5, 9.5)
plt.show()
# 資料
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
# 套用Scikit-Learn Estimator API
from sklearn.manifold import Isomap
model = Isomap(n_components = 2)
model.fit(X_digits)
X_projected = model.transform(X_digits)
# 檢視預測的成分和真正的類別之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X_projected[:, 0], X_projected[:, 1], c = y_digits, edgecolor = "none", alpha = 0.5, cmap = plt.cm.get_cmap("cubehelix", 10))
plt.colorbar(label = "Digit Label", ticks = range(10))
plt.clim(-0.5, 9.5)
plt.show()
l 非監督式學習-集群-k-平均集群法(k-means Clustering):
# 資料
from sklearn.datasets import load_iris
iris = load_iris()
X_iris = iris.data
y_iris = iris.target
# 把資料分為訓練集(Training Set)與測試集(Testing Set)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_iris, y_iris, random_state = 0)
# 套用Scikit-Learn Estimator API
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors = 1)
model.fit(X_train, y_train)
y_fit = model.predict(X_test)
# 檢視預測的分類和真正的類別符合之比率
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_fit))
# 資料
from sklearn.datasets import load_iris
iris = load_iris()
X_iris = iris.data
y_iris = iris.target
# 把資料分為訓練集(Training Set)與測試集(Testing Set)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_iris, y_iris, random_state = 0)
# 套用Scikit-Learn Estimator API
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors = 1)
model.fit(X_train, y_train)
y_fit = model.predict(X_test)
# 檢視預測的分類和真正的類別符合之比率
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_fit))
l 非監督式學習-集群-高斯混合模型(Gaussian Mixture Model, GMM):
# 資料
import seaborn as sns
iris = sns.load_dataset("iris")
X_iris = iris.drop("species", axis = 1)
y_iris = iris["species"]
# 主成分分析後的資料
from sklearn.decomposition import PCA
PCAModel = PCA(n_components = 2)
PCAModel.fit(X_iris)
X_projected = PCAModel.transform(X_iris)
iris["PCA1"] = X_projected[:, 0]
iris["PCA2"] = X_projected[:, 1]
# 套用Scikit-Learn Estimator API
from sklearn.mixture import GaussianMixture
model = GaussianMixture(n_components = 3, covariance_type = "full")
model.fit(X_iris)
y_fit = model.predict(X_iris)
# 檢視預測的分類和真正的類別之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
iris["cluster"] = y_fit
sns.lmplot("PCA1", "PCA2", data = iris, hue = "species", col = "cluster", fit_reg = False)
plt.show()
# 資料
import seaborn as sns
iris = sns.load_dataset("iris")
X_iris = iris.drop("species", axis = 1)
y_iris = iris["species"]
# 主成分分析後的資料
from sklearn.decomposition import PCA
PCAModel = PCA(n_components = 2)
PCAModel.fit(X_iris)
X_projected = PCAModel.transform(X_iris)
iris["PCA1"] = X_projected[:, 0]
iris["PCA2"] = X_projected[:, 1]
# 套用Scikit-Learn Estimator API
from sklearn.mixture import GaussianMixture
model = GaussianMixture(n_components = 3, covariance_type = "full")
model.fit(X_iris)
y_fit = model.predict(X_iris)
# 檢視預測的分類和真正的類別之繪圖
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
iris["cluster"] = y_fit
sns.lmplot("PCA1", "PCA2", data = iris, hue = "species", col = "cluster", fit_reg = False)
plt.show()
特徵工程(Feature Engineering)
l 在真實的世界中,資料很少是簡潔的數值資料,因此需要特徵工程。
l 分類特徵:
data = [{"price": 850000, "rooms": 4, "neighborhood": "Queen Anne"},
{"price": 700000, "rooms": 3, "neighborhood": "Fremont"},
{"price": 650000, "rooms": 3, "neighborhood": "Wallingford"},
{"price": 600000, "rooms": 2, "neighborhood": "Fremont"}]
# 以One-hot Encoding為類別資料建立額外欄位
from sklearn.feature_extraction import DictVectorizer
# sparse = True稀疏輸出(Sparse Output),用來解決資料集巨幅增加的情形
aVec = DictVectorizer(sparse = False, dtype = int)
print(aVec.fit_transform(data))
print(aVec.get_feature_names())
data = [{"price": 850000, "rooms": 4, "neighborhood": "Queen Anne"},
{"price": 700000, "rooms": 3, "neighborhood": "Fremont"},
{"price": 650000, "rooms": 3, "neighborhood": "Wallingford"},
{"price": 600000, "rooms": 2, "neighborhood": "Fremont"}]
# 以One-hot Encoding為類別資料建立額外欄位
from sklearn.feature_extraction import DictVectorizer
# sparse = True稀疏輸出(Sparse Output),用來解決資料集巨幅增加的情形
aVec = DictVectorizer(sparse = False, dtype = int)
print(aVec.fit_transform(data))
print(aVec.get_feature_names())
l 文字特徵:
data = ["problem of evil", "evil queen", "horizon problem"]
from sklearn.feature_extraction.text import CountVectorizer
aVec = CountVectorizer()
a = aVec.fit_transform(data)
b = aVec.get_feature_names()
import pandas as pd
c = pd.DataFrame(a.toarray(), columns = b)
print(c)
# 原始字數計算會導致特徵被放太多權重在非常高頻出現的字上
# 修正此問題方法為Term Frequency-inverse Document Frequency(TF-IDF)
from sklearn.feature_extraction.text import TfidfVectorizer
bVec = TfidfVectorizer()
d = bVec.fit_transform(data)
e = bVec.get_feature_names()
f = pd.DataFrame(d.toarray(), columns = e)
print(f)
data = ["problem of evil", "evil queen", "horizon problem"]
from sklearn.feature_extraction.text import CountVectorizer
aVec = CountVectorizer()
a = aVec.fit_transform(data)
b = aVec.get_feature_names()
import pandas as pd
c = pd.DataFrame(a.toarray(), columns = b)
print(c)
# 原始字數計算會導致特徵被放太多權重在非常高頻出現的字上
# 修正此問題方法為Term Frequency-inverse Document Frequency(TF-IDF)
from sklearn.feature_extraction.text import TfidfVectorizer
bVec = TfidfVectorizer()
d = bVec.fit_transform(data)
e = bVec.get_feature_names()
f = pd.DataFrame(d.toarray(), columns = e)
print(f)
l 缺失資料的插補(Imputation):
import numpy as np
from numpy import nan
X = np.array([[nan, 0, 3], [3, 7, 9], [3, 5, 2], [4, nan, 6], [8, 8, 1]])
print(X)
from sklearn.impute import SimpleImputer
imp = SimpleImputer(strategy = "mean")
X2 = imp.fit_transform(X)
print(X2)
import numpy as np
from numpy import nan
X = np.array([[nan, 0, 3], [3, 7, 9], [3, 5, 2], [4, nan, 6], [8, 8, 1]])
print(X)
from sklearn.impute import SimpleImputer
imp = SimpleImputer(strategy = "mean")
X2 = imp.fit_transform(X)
print(X2)
l 推導的特徵(Derived Features):
import numpy as np
X = np.array([1, 2, 3, 4, 5])[:, np.newaxis]
y = np.array([4, 2, 1, 3, 7])
# 產生推導的特徵
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree = 3, include_bias = False)
X2 = poly.fit_transform(X)
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(X2, y)
y2_fit = model.predict(X2)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X, y)
plt.plot(X, y2_fit)
plt.show()
import numpy as np
X = np.array([1, 2, 3, 4, 5])[:, np.newaxis]
y = np.array([4, 2, 1, 3, 7])
# 產生推導的特徵
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree = 3, include_bias = False)
X2 = poly.fit_transform(X)
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(X2, y)
y2_fit = model.predict(X2)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X, y)
plt.plot(X, y2_fit)
plt.show()
l 特徵管線:
import numpy as np
X = np.array([1, 2, 3, 4, 5])[:, np.newaxis]
y = np.array([4, 2, 1, 3, 7])
X2 = np.linspace(-0.1, 5.1, 500)[:, np.newaxis]
# 讓處理成為平行的管線
# 推導二階方程式特徵 + 擬合線性迴歸
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
model = make_pipeline(PolynomialFeatures(degree = 2), LinearRegression())
model.fit(X, y)
y2_fit = model.predict(X2)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X, y)
plt.plot(X2, y2_fit)
plt.show()
import numpy as np
X = np.array([1, 2, 3, 4, 5])[:, np.newaxis]
y = np.array([4, 2, 1, 3, 7])
X2 = np.linspace(-0.1, 5.1, 500)[:, np.newaxis]
# 讓處理成為平行的管線
# 推導二階方程式特徵 + 擬合線性迴歸
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
model = make_pipeline(PolynomialFeatures(degree = 2), LinearRegression())
model.fit(X, y)
y2_fit = model.predict(X2)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X, y)
plt.plot(X2, y2_fit)
plt.show()
模型驗證(Model Validation)
l 透過Cross-validation進行模型驗證:
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
from sklearn.model_selection import train_test_split
X1, X2, y1, y2 = train_test_split(X_digits, y_digits, random_state = 0, train_size = 0.5)
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors = 1)
# Two-fold Cross-validation方法一
y2_fit = model.fit(X1, y1).predict(X2)
y1_fit = model.fit(X2, y2).predict(X1)
from sklearn.metrics import accuracy_score
print(accuracy_score(y1, y1_fit))
print(accuracy_score(y2, y2_fit))
# Two-fold Cross-validation方法二
from sklearn.model_selection import cross_val_score
print(cross_val_score(model, X_digits, y_digits, cv = 2))
# Five-fold Cross-validation
print(cross_val_score(model, X_digits, y_digits, cv = 5))
# Leave-one-out Cross-validation訓練資料時只留下一個資料做為驗證之用
from sklearn.model_selection import LeaveOneOut
scores = cross_val_score(model, X_digits, y_digits, cv = LeaveOneOut())
print(scores)
print(scores.mean())
from sklearn.datasets import load_digits
digits = load_digits()
X_digits = digits.data
y_digits = digits.target
from sklearn.model_selection import train_test_split
X1, X2, y1, y2 = train_test_split(X_digits, y_digits, random_state = 0, train_size = 0.5)
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors = 1)
# Two-fold Cross-validation方法一
y2_fit = model.fit(X1, y1).predict(X2)
y1_fit = model.fit(X2, y2).predict(X1)
from sklearn.metrics import accuracy_score
print(accuracy_score(y1, y1_fit))
print(accuracy_score(y2, y2_fit))
# Two-fold Cross-validation方法二
from sklearn.model_selection import cross_val_score
print(cross_val_score(model, X_digits, y_digits, cv = 2))
# Five-fold Cross-validation
print(cross_val_score(model, X_digits, y_digits, cv = 5))
# Leave-one-out Cross-validation訓練資料時只留下一個資料做為驗證之用
from sklearn.model_selection import LeaveOneOut
scores = cross_val_score(model, X_digits, y_digits, cv = LeaveOneOut())
print(scores)
print(scores.mean())
l 偏差和變異的權衡:
# Degree-1多項式:y = ax + b
# Degree-3多項式:y = ax3 + bx2 + cx + d
# 低度擬合(Underfit)的資料具有高度偏差(Bias),例如最佳情況為使用Degree-3多項式擬合資料,卻使用Degree-1多項式
# 過度擬合(Overfit)的資料具有高度變異(Variance),例如最佳情況為使用Degree-3多項式擬合資料,卻使用Degree-9多項式
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
X_test = np.linspace(-0.1, 1.1, 500)[:, np.newaxis]
# 擬合不同階數多項式並視覺化資料
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X.ravel(), y, color = "black")
for degree in [1, 3, 5]:
y_test = PolynomialRegression(degree).fit(X, y).predict(X_test)
plt.plot(X_test, y_test, label = "Degree = {0}".format(degree))
plt.xlim(-0.1, 1.1)
plt.ylim(-2, 12)
plt.legend(loc = "best")
plt.show()
# Degree-1多項式:y = ax + b
# Degree-3多項式:y = ax3 + bx2 + cx + d
# 低度擬合(Underfit)的資料具有高度偏差(Bias),例如最佳情況為使用Degree-3多項式擬合資料,卻使用Degree-1多項式
# 過度擬合(Overfit)的資料具有高度變異(Variance),例如最佳情況為使用Degree-3多項式擬合資料,卻使用Degree-9多項式
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
X_test = np.linspace(-0.1, 1.1, 500)[:, np.newaxis]
# 擬合不同階數多項式並視覺化資料
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X.ravel(), y, color = "black")
for degree in [1, 3, 5]:
y_test = PolynomialRegression(degree).fit(X, y).predict(X_test)
plt.plot(X_test, y_test, label = "Degree = {0}".format(degree))
plt.xlim(-0.1, 1.1)
plt.ylim(-2, 12)
plt.legend(loc = "best")
plt.show()
l 驗證曲線(Validation Curve):
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
# 視覺化驗證曲線,此例以多項式階數控制模型複雜度
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
import seaborn as sns
degree = np.arange(0, 21)
train_score, val_score = validation_curve(PolynomialRegression(), X, y, "polynomialfeatures__degree", degree, cv = 7)
sns.set()
plt.plot(degree, np.median(train_score, axis = 1), color = "blue", label = "Training Score")
plt.plot(degree, np.median(val_score, axis = 1), color = "red", label = "Validation Score")
plt.legend(loc = "best")
plt.ylim(0, 1)
plt.xlabel("Degree")
plt.ylabel("Score")
plt.show()
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
# 視覺化驗證曲線,此例以多項式階數控制模型複雜度
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
import seaborn as sns
degree = np.arange(0, 21)
train_score, val_score = validation_curve(PolynomialRegression(), X, y, "polynomialfeatures__degree", degree, cv = 7)
sns.set()
plt.plot(degree, np.median(train_score, axis = 1), color = "blue", label = "Training Score")
plt.plot(degree, np.median(val_score, axis = 1), color = "red", label = "Validation Score")
plt.legend(loc = "best")
plt.ylim(0, 1)
plt.xlabel("Degree")
plt.ylabel("Score")
plt.show()
l 學習曲線(Learning Curve):
# 從較大的資料集中計算的驗證曲線可以支援更複雜的模型
# 以資料集的大小繪製訓練分數與驗證分數的圖形稱為學習曲線
# 增加學習曲線收斂分數的唯一方法是使用不同的模型
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
# 視覺化學習曲線
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import learning_curve
sns.set()
fig, ax = plt.subplots(1, 2, figsize = (16, 6))
fig.subplots_adjust(left = 0.0625, right = 0.95, wspace = 0.1)
for i, degree in enumerate([2, 9]):
num, train_lc, val_lc = learning_curve(PolynomialRegression(degree), X, y, cv = 7, train_sizes = np.linspace(0.1, 1, 32))
ax[i].plot(num, np.mean(train_lc, axis = 1), color = "blue", label = "Training Score")
ax[i].plot(num, np.mean(val_lc, axis = 1), color = "red", label = "Validation Score")
ax[i].hlines(np.mean([train_lc[-1], val_lc[-1]]), num[0], num[-1], color = "gray", linestyle = "dashed")
ax[i].set_xlim(num[0], num[-1])
ax[i].set_ylim(0, 1)
ax[i].set_xlabel("Training Size")
ax[i].set_ylabel("Score")
ax[i].set_title("Degree = {0}".format(degree), size = 14)
ax[i].legend(loc = "best")
plt.show()
# 從較大的資料集中計算的驗證曲線可以支援更複雜的模型
# 以資料集的大小繪製訓練分數與驗證分數的圖形稱為學習曲線
# 增加學習曲線收斂分數的唯一方法是使用不同的模型
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
# 視覺化學習曲線
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import learning_curve
sns.set()
fig, ax = plt.subplots(1, 2, figsize = (16, 6))
fig.subplots_adjust(left = 0.0625, right = 0.95, wspace = 0.1)
for i, degree in enumerate([2, 9]):
num, train_lc, val_lc = learning_curve(PolynomialRegression(degree), X, y, cv = 7, train_sizes = np.linspace(0.1, 1, 32))
ax[i].plot(num, np.mean(train_lc, axis = 1), color = "blue", label = "Training Score")
ax[i].plot(num, np.mean(val_lc, axis = 1), color = "red", label = "Validation Score")
ax[i].hlines(np.mean([train_lc[-1], val_lc[-1]]), num[0], num[-1], color = "gray", linestyle = "dashed")
ax[i].set_xlim(num[0], num[-1])
ax[i].set_ylim(0, 1)
ax[i].set_xlabel("Training Size")
ax[i].set_ylabel("Score")
ax[i].set_title("Degree = {0}".format(degree), size = 14)
ax[i].legend(loc = "best")
plt.show()
l 格狀搜尋(Grid Search):
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
X_fit = np.linspace(-0.1, 1.1, 500)[:, np.newaxis]
# 格狀搜尋模型
from sklearn.model_selection import GridSearchCV
# 如果最佳值落在邊界上,就需要拓展這個格子以確保真的找到最佳值
param_grid = {"polynomialfeatures__degree": np.arange(21),
"linearregression__fit_intercept": [True, False],
"linearregression__normalize": [True, False]}
grid = GridSearchCV(PolynomialRegression(), param_grid, cv = 7)
# 詢問最佳參數
grid.fit(X, y)
print(grid.best_params_)
# 使用最佳模型並視覺化資料
model = grid.best_estimator_
y_fit = model.fit(X, y).predict(X_fit)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X.ravel(), y, color = "black")
plt.plot(X_fit.ravel(), y_fit)
plt.xlim(-0.1, 1.1)
plt.ylim(-2, 12)
plt.show()
# 多項式模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree = 2, **kwargs):
a = PolynomialFeatures(degree)
b = LinearRegression(**kwargs)
return make_pipeline(a, b)
# 建立一些用來擬合模型的資料
import numpy as np
def make_data(N, err = 1, rseed = 1):
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1 / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
X, y = make_data(40)
X_fit = np.linspace(-0.1, 1.1, 500)[:, np.newaxis]
# 格狀搜尋模型
from sklearn.model_selection import GridSearchCV
# 如果最佳值落在邊界上,就需要拓展這個格子以確保真的找到最佳值
param_grid = {"polynomialfeatures__degree": np.arange(21),
"linearregression__fit_intercept": [True, False],
"linearregression__normalize": [True, False]}
grid = GridSearchCV(PolynomialRegression(), param_grid, cv = 7)
# 詢問最佳參數
grid.fit(X, y)
print(grid.best_params_)
# 使用最佳模型並視覺化資料
model = grid.best_estimator_
y_fit = model.fit(X, y).predict(X_fit)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.scatter(X.ravel(), y, color = "black")
plt.plot(X_fit.ravel(), y_fit)
plt.xlim(-0.1, 1.1)
plt.ylim(-2, 12)
plt.show()










沒有留言:
張貼留言